国家天元数学西北中心定于5月7日-9日在线举办“流体力学方程组自由边界问题研讨班”。该研讨班为中心2020“偏微分方程与油气勘探”主题年活动之一。该活动的首席科学家为江松院士,西北大学郭真华教授为活动召集人。研讨班邀请一线专家研讨与油气勘探有关的流体力学方程组自由边界问题,包括自由边界条件的精确描述,油、气、水物理边界上的数值边界条件确定方法,自由边界问题如何转化为固定边值等问题,以期发展用于油气勘探的更有效的数值模拟方法。
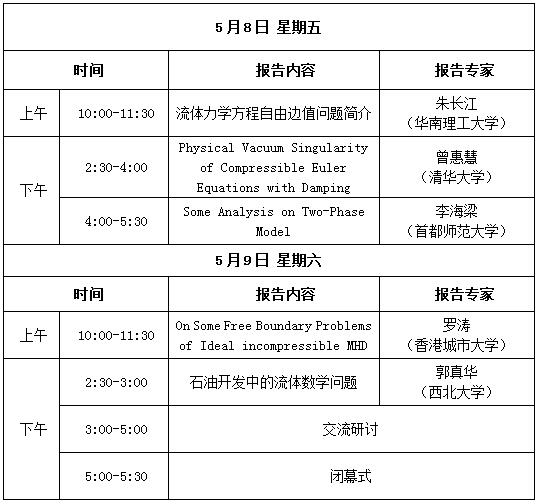
一、专题研讨班日程安排
时间:2020年5月7日-9日

二、报名方式:
全国高等院校从事偏微分方程与油气勘探相关的应用数学交叉领域的青年教师及在校研究生均可报名参加。为统计参会人数、及时通知会议信息,请有意参加的学者通过链接或扫描学员报名表二维码填写报名表:https://docs.qq.com/form/fill/DZWFzRWNHdmhkTHdo?_w_tencentdocx_form=1并于5月3日(周日)前提交。并扫描下方二维码加入微信学员群。


三、参会方式:
本次专题研讨班使用“腾讯会议”视频软件,为避免一些突发情况,我们将ZOOM视频会议软件作为备用,并通过微信群与您及时联系,请您提前调试好设备。
1. 腾讯会议链接 (请您按日期进入当日的会议室)
5月7日
会议时间:2020/5/7 08:00-22:00
会议链接:https://meeting.tencent.com/s/53hq0na3b1c8
会议 ID:217 165 907
5月8日
会议时间:2020/5/8 08:00-22:00
会议链接:https://meeting.tencent.com/s/5mArXwu0d5f8
会议 ID:595 354 011
5月9日
会议时间:2020/5/9 08:00-22:00
会议链接:https://meeting.tencent.com/s/5cCeOMub91bc
会议 ID:547 432 118
2. ZOOM 会议室(备用)
会议时间:5月7日-9日
加入 Zoom 会议
https://zoom.com.cn/j/6550493543?pwd=V0ZPVWlIR2UydmVQSUxoNUNTQU5qdz09
会议 ID:655 049 3543
四、专家简介及报告内容:(按报告顺序)
1. 报告专家:Dehua Wang 教授 University of Pittsburgh
个人简介:I am currently a professor at the University of Pittsburgh. I received my B.S. degree from Tsinghua University (Beijing) and Ph.D. degree from the University of Chicago. My research field is partial differential equations and applied mathematics.
报告题目:Some mathematical problems on active hydrodynamics
报告内容:Active hydrodynamics describes fluids with active constituent particles that have collective motion and are constantly maintained out of equilibrium by internal energy sources, rather than by the external forces applied to the system. In particular, when the particles have elongated shapes, usually the collective motion induces the particles to demonstrate orientational ordering at high concentration, and thus there are natural analogies with nematic liquid crystals. Active hydrodynamics has wide applications and have attracted much attention in recent decades. In this talk, I will present some mathematical results on the existence and regularity of global solutions to the equations governing the active hydrodynamics and discuss some open problems related to the Cauchy problem, initial-boundary value problem and free boundary problem.
2. 报告专家:谢春景 教授 上海交通大学
个人简介:谢春景,2011年加入上海交通大学,先后担任副教授、教授。在香港中文大学获得博士学位,曾先后在香港中文大学和密西根大学做博士后。主要研究兴趣为定常流及其相关模型的适定性。
报告题目:Subsonic and Transonic Solutions for the Euler System with Free Boundaries
报告内容:The study on steady Euler system involves quite a few difficulty issues, such as mixed type equations, the corner singularity near the physical boundaries. In this talk, we mainly focus on transonic shock solutions and subsonic solutions for the Euler system with free boundaries.
3. 报告专家:王筱平 教授 香港科技大学
个人简介:王教授于1984年获得北京大学数学学士学位,并于1990年从库朗研究所(NYU)获得博士学位。他曾在伯克利的MSRI和科罗拉多大学担任博士后。王教授现为香港科技大学数学系主任。他还是香港工业与应用数学学会主席。王教授目前的研究兴趣是:界面问题和多相流的建模与模拟;图像处理;微磁计算的数值方法。他于2007年获得冯康科学计算奖,他是2016年SIAM材料科学数学会议和2019年国际工业和应用数学大会的大会报告人。
报告题目:Introduction of Threshold Dynamics Method for Interface Motion
报告内容:The threshold dynamics method developed by Merriman, Bence and Osher (MBO) is an efficient method for simulating the motion by mean curvature flow. The method is based on the observation that the level-set of the solution of a heat equation moves in normal direction at a velocity equal to the mean curvature of the level-set surface. The method alternately diffuses and sharpens characteristic functions of regions and is easy to implement and highly efficient. I will give an introduction of the threshold dynamics method and its generalizations. Applications to the interface motion in multiphase flow, network formation and image processing will also be presented.
4. 报告专家:杜力力 教授 四川大学
个人简介:杜力力,1978年2月出生,男,四川成都人,2005年获得四川大学应用数学博士学位。现任四川大学数学学院教授,博士生导师。2006年至2008年,中山大学数学学院博士后;2008年至2009年香港中文大学数学科学研究所博士后;2010年就职于四川大学,并工作至今。从事非线性偏微分方程及其应用的研究工作,在高维可压缩Euler方程组的适定性、Bernoulli型自由边界问题等研究领域取得了一系列的结果,在Arch. Rational Mech. Anal., Comm. Math. Phys., Tran. AMS., Comm. PDEs,Calculus of Variations and PDEs等国际学术刊物发表学术论文40余篇。
报告题目:椭圆方程自由边界问题及其在流体力学中的应用
报告内容:我们将介绍两个典型的椭圆方程自由边界问题的数学理论,即障碍物型自由边界问题与Bernoulli型自由边界问题的适定性理论。进一步,我们将详细介绍Bernoulli型自由边界问题在流体力学中的应用,特别是在不可压缩与可压缩定常理想喷流,冲击喷流问题适定性理论中的应用。
5. 报告专家:朱长江 教授 华南理工大学
个人简介:朱长江,博士,教授,博士生导师,国际数学学术期刊《Kinetic and Related Models》、《Acta Mathematica Scientia》、《数学物理学报》等杂志编委,《数学教育学报》副主编,教育部高等学校数学类教学指导委员会委员,教育部“创新团队发展计划”、国家自然科学基金重点项目、国家级教学团队、国家级精品课程和国家精品资源共享课程负责人,全国百篇优秀博士学位论文指导教师。主持完成的研究成果获教育部自然科学奖二等奖,教学成果两次获国家级教学成果奖二等奖。2012年被评为全国优秀科技工作者。
报告题目:流体力学方程自由边值问题简介
报告内容:本次报告将以一维Navier-Stokes方程为例,简要介绍自由边值问题,内容包括:自由边界的提法以及自由边值问题的形成;如何将自由边值问题化为固定边值问题;一维Navier-Stokes方程自由边值问题的研究进展;相关模型自由边值问题的研究进展等。
6. 报告专家:曾惠慧 教授 清华大学
个人简介:曾惠慧,清华大学丘成桐数学科学中心及数学科学系教授,从事偏微分方程研究。2009年在香港中文大学取得博士学位,其博士论文获香港数学学会最佳论文奖,毕业后曾在美国乔治城大学和哈佛大学做博士后。2012年开始在清华大学工作,2015年获清华大学学术新人奖。曾惠慧教授近期主要研究兴趣为流体力学中偏微分方程的自由边界问题。研究成果发表于 Comm. Pure Appl. Math., Arch. Rational Mech. Anal., Adv. Math.及Comm. Math. Phys.等学术期刊。
报告题目:Physical Vacuum Singularity of Compressible Euler Equations with Damping
报告内容:For vacuum free boundary problems of compressible fluids, the physical vacuum singularity of the sound speed being of ½ Holder but not Lipshitzian continuous near vacuum states as a characteristic phenomenon appearing in some important physical situations, such as gaseous stars, compressible flows with damping and shallow waters. The physical singularity near vacuum states prevents the standard method of symmetric systems developed by Friedrichs-Lax-Kato-Kreiss from applying. In this talk, I will discuss the global and almost global solutions to the vacuum free boundary problems with the physical vacuum singularity of compressible Euler equations with damping in the 1-D and 3-D cases, respectively.
7. 报告专家:李海梁 教授 首都师范大学
个人简介:李海梁教授,1999年于中国科学院数学研究所获得博士学位;偏微分方程专家,博士生导师,现任首都师范大学数学科学院院长。长期致力于非线性偏微分方程数学理论的研究,包括可压缩流体方程和Kinetic方程等,重点研究解的适定和性态分析等,取得了一系列有重要意义的创新成果,被国内外权威学术刊物(如Comm. Math. Phys., Arch. Ration. Mech. Anal., SIAM J.Math. Anal.,等)接受发表,对相关问题的研究产生了重要影响,受到国内外专家的好评。先后入选北京市“科技新星”计划(2005年)、教育部“新世纪优秀人才支持计划”(2007年)。荣获霍英东基金会“第十一届高校青年教师基金”资助(2008年)。
报告题目:Some Analysis on Two-phase Model
报告内容:The subject of multi-phase flow has become increasingly important in a wide variety of applied scientific areas including industries and engineering systems to simulate, for instance, the process like sprays, waste water treatment, oil-gas mixing, and Diesel engines etc. In this talk, we consider the two protype of two-phase models, the fluid-particle model and drift-flux model. We first introduce some progress on these two-phase models flows, and present our recent results on the stability of steady-state of in-flow/out-flow for drift-flux model, and the nonlinear stability of rarefaction waves, long time of liquid-gas model.
8. 报告专家:罗涛 教授 香港城市大学
个人简介:罗涛教授于1995年于中国科学院数学研究所获得博士学位。 后于美国密西根大学(University of Michigan), Georgetown University (乔治城大学) 历任助理教授, 副教授 ,及教授。 于2016年至今于香港城市大学任教授。罗涛教授的主要研究领域为流体力学中的非线性偏微分方程, 如Euler 及 Navier-Stokes方程。 近期主要研究兴趣为流体力学及磁流体中非线性偏微分方程的自由边界问题。研究成果发表于 Comm. Pure Appl. Math., Arch. Rational Mech. Anal., Comm. Math. Phys., Adv. In. Math. 等学术刊物。
报告题目:On Some Free Boundary Problems of Ideal Incompressible MHD
报告内容:In the first part of the lecture, I will discuss some results on the ill-posedness for a free boundary problem of ideal incompressible MHD when the Taylor sign condition is violated, from linear ill-posedness to nonlinear ill-posedness.
In the second part of the lecture, I will discuss results on linearized well-posedness for a free boundary problem of ideal incompressible MHD when the Taylor sign condition is satisfied.
For both problems, the free boundary is a moving closed curve (in two-dimensions) and a closed surface (in three dimensions).
The aim is to illustrate the importance of the Taylor sign condition to the well-posedness and stability of ideal incompressible when the free boundary is a closed surface or curve, in contrast to the case when the free surface is a graph.
This talk is based on the joint work with Chengchun Hao.
9. 报告专家:郭真华 教授 西北大学
报告题目:石油开发中的流体数学问题
报告内容:本报告主要介绍与在石油中与流体力学方程相关的数学理论与数值计算问题,涉及气、液两相流和三相流模型。
五、联系方式
联系人:白老师
办公电话:029-82665627
邮箱:xbty@xjtu.edu.cn
地址:西安交通大学数学与统计学院111办公室