为推动国内拓扑学方向的合作与交流,国家天元数学西北中心定于2019年9月20日(周五)-9月22日(周日)在西安交通大学数学楼二楼2-1会议室举行“西安几何拓扑研讨会”。本次会议特邀北京大学姜伯驹院士、王诗宬院士等国内60多名拓扑学专家学者,就几何拓扑领域的最新进展进行研讨。
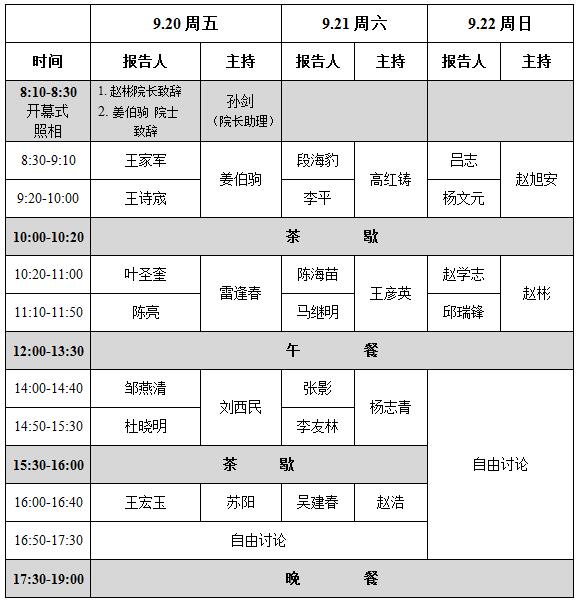
会议日程
会议联系人:张老师 Email:zhangq.math@xjtu.edu.cn
报告题目、摘要
陈海苗(北京工商大学)
题目:Representation varieties and character varieties of links

陈亮(东北师范大学)
题目:Legendrian duality and its applications
摘要:We first introduce a basic Legendrian duality among pseudo spheres in semi-Euclidean space. As its applications, I will investigate caustics of the fronts in 2-dimensional hyperbolic space and singularities of Gauss maps of the degenerate surfaces in 4-dimensional Anti de Sitter space.
杜晓明(华南理工大学)
标题:不可定向曲面映射类群以及 Dehn twist 子群的有限阶生成元集
Title: The torsion generating set of the mapping class groups and Dehn twist subgroups of non-orientable surfaces
摘要:设Ng是亏格为g的不可定向曲面,我们证明当g=7,11,14…时,Ng的映射类群可被3个有限阶元素生成;当g=9,13,17…时,Ng的映射类群中的 Dehn twist 子群可被3个有限阶元素生成。

段海豹(中国科学院)
题目:On the multi-degree of coverings on Lie groups
摘要:For a Lie group G with center Z(G) consider the covering map c:G→PG:=G/Z(G). The induced map c^{∗}:H^{∗}(PG)→H^{∗}(G) on the integral cohomologies gives rise to a sequence D(G;PG) of integers, called the multi-degree of the covering c. We determine the sequence D(G;PG) for all 1-connected simple Lie groups with non-trivial centers.
李平(同济大学)
题目: The rigidity on the second fundamental form of projective manifolds
摘要:We review some known gap phenomena related to the second fundamental form of the minimal submanfolds and complex submanifolds in the unit spheres and complex projective spaces respectively, and then present our recent progress on them.
李友林(上海交通大学)
题目: Smoothly non-isotopic Lagrangian disk fillings of Legendrian knots
摘要: In this talk, we construct families of distinct Lagrangian ribbon disks in the standard symplectic 4-ball which have the same boundary Legendrian knots, and are not smoothly isotopic or have non-homeomorphic exteriors. This is joint work with Motoo Tange.
吕志(复旦大学)
题目:On orbit braids
摘要:Let M be a connected topological manifold of dimension at least 2 with an effective action of a finite group G. Associating with the orbit configuration space F_G(M, n), n ≥ 2 of the G-manifold M, we try to upbuild the theoretical framework of orbit braids in M × I where the action of G on I is trivial, which contains the following contents: we introduce the orbit braid group B_n^{orb}(M, G), and show that it is isomorphic to a group with an additional endowed operation (called the extended fundamental group), formed by the homotopy classes of some paths (not necessarily closed paths) in F_G(M, n), which is an essential extension for fundamental groups. The orbit braid group B_n^{orb}(M, G) is large enough to contain the fundamental group of F_G(M, n) and other various braid groups as its subgroups. Around the central position of B_n^{orb}(M, G), we obtain five short exact sequences weaved in a commutative diagram. We also analyze the essential relations among various braid groups associated to those configuration spaces F_G(M, n), F(M, n), and F(M/G, n). We finally consider how to give the presentations of orbit braid groups in terms of orbit braids as generators. We carry out our work by choosing M = ℂ ≈ ℝ2 with typical actions of ℤp and (ℤ2)2. We obtain the presentations of the corresponding orbit braid groups, from which we see that the generalized braid group Br(Dn) (introduced by Brieskorn) actually agrees with the orbit braid group B_n^{orb}(ℂ\{0}, ℤ2) and Br(Dn) is a subgroup of the orbit braid group B_n^{orb}(ℂ, ℤ2). This talk is based upon a joint work with Hao Li and Fengling Li.
马继明(复旦大学)
题目: Compact 4-dimensional hyperbolic Coxeter polytopes with eight facets
摘要: We give the classification of all the compact 4-dimensional hyperbolic Coxeter polytopes with eight facets, the proof uses geometrical, combinatorial, and computational techniques. This is a joint work with Fangting Zheng.
邱瑞锋(华东师范大学)
题目:Heegaard splitting, a survey.
摘要:TBA
王宏玉(扬州大学)
题目:On signed Euler Characteristic
摘要:In this talk, we discuss the Chern-Hopf conjecture. Let M be a closed symplectic manifold of dimension 2n with non-ellipticity. We can de ne an almost Kahler structure on M by using the given symplectic form. Using Darboux coordinate charts, we deform the given almost Kahler structure to obtain a homotopy equivalent Lipschitz Kahler structure on the universal covering of M. Analogous to Teleman's L2-Hodge decomposition on PL manifolds or Lipschitz Riemannian manifolds, we give a L2-Hodge decomposition theorem on the universal covering of M w.r.t. the measurable Kahler metric. Using an argument of Gromov, we give a vanishing theorem for L2 harmonic p-forms, p 6= n (resp. a non-vanishing theorem for L2 harmonic n-forms) on the universal covering of M which is d(sublinear) (resp. d(bounded)), then its signed Euler characteristic satisfies (1)n­(M) 0 (resp. (1)n­(M) > 0). As an application, we show that the Chern-Hopf conjecture holds true in closed even dimensional Riemannian manifolds with nonpositive curvature (resp. strictly negative curvature), it gives a positive answer to a Yau's problem due to S. S. Chern and H. Hopf.
王家军(北京大学)
TBA
王诗宬(北京大学)
题目:Some remarks on extending periodical maps on surfaces
吴建春(苏州大学)
题目: GL_d(\Z)中的一些算法问题
摘要: 介绍一些几何群论尤其是关于一般线性群GL_d(\Z)的算法问题。
杨文元(北京大学)
题目:Martin boundary of random walks on groups
摘要:我们将介绍群上的随机游走的基本概念和理论,侧重于带非正曲率的群的Possion边界和Martin边界的确定问题。我们将介绍双曲群,相对双曲群的已知的结果,以及正在进行的带收缩元素的群的一些相关工作介绍。
叶圣奎(西交利物浦大学)
题目: Rigidity of matrix group actions on CAT(0) spaces with possible parabolic isometries
摘要: It is well-known that SLn(Qp) acts without fixed points on an (n-1)- dimensional CAT(0) space (the affine building). We prove that n-1 is the smallest dimension of CAT(0) spaces on which matrix groups act without fixed points. Explicitly, let R be an associative ring with identity and E_n(R) the extended elementary subgroup. Any isometric action of E_n(R) on a complete CAT(0) space X^d of dimension d < n-1 has a fixed point. Similar results are discussed for automorphism groups of free groups.
张影(苏州大学)
题目: Comparison of minimal equal lengths in a once punctured torus running over its relative Teichmuller space
摘要: We consider the problem of minimizing the equal length of a pair of simple closed geodesics of given topological type in a once punctured hyperbolic torus with fixed geometric boundary data as the torus runs over its relative Teichmuller space. For specific pairs with symmetry, we are able to determine the minimizing torus and hence the minimal length. It is natural to compare the minimal lengths for inequivalent pair of the same intersection number. As computer experiments show, there is a conjecture that the specific pair of slopes (1/0, 1/n) has its minimal length smaller than any other pair of slopes (1/0, m/n), regardless of the geometric boundary data. In joint work with Da Lei, we obtain a stronger result as the geometric boundary of the torus is a conic point and the cone angle is approaching $2\pi$.
赵学志(首都师范大学)
题目:Geometric intersections numbers of loops on surfaces
摘要:Given two loops on a compact surfaces $F$, it is natural to ask: what is their minimal intersection number during homotopy classes? This number is usually said to be the geometric intersection number. In this talk, we shall explain a way to determine the geometric intersection and self-intersection numbers of loops on surfaces. Our integration are Nielsen fixed point theory and Gr\"{o}bner-Shirsov basis. We illustrate an application: An algorithm to compute the distance of loops in curve complex. This talk includes a joint work with Gu Ying.
邹燕清(大连民族大学)
题目:Mapping class group of a Heegaard splitting
摘要:We will introduce some recent results on mapping class group of a Heegaard splitting.