【暑期学校简介】
一带一路代数几何暑期学校由国家天元数学西北中心主办、新疆大学数学与系统科学学院和伊犁师范大学数学学院联合承办,旨在为全国及一带一路沿线高年级优秀本科生、研究生提供代数、几何等领域的学术交流平台。暑期学校课程涵盖了代数、几何的基本理论,研究方法和前沿动态,包括代数表示、复几何等内容。学员们将与国内专家进行面对面的交流,分享彼此的研究成果和经验,拓宽学术视野。
课程内容及主题如下:
1. 代数专题和几何专题讲习班,各组织24课时。代数专题讲习班讲解箭图表示(quiver representation)表示等基础理论;几何专题讲习班传授微分流形、黎曼几何、子流形以及几何分析等基础理论。
2. 组织代数、几何相关的前沿学术报告和研讨4场。
【委员会】
专家委员会:
朱 彬 教授 清华大学
程新跃 教授 重庆师范大学
辛 巧 教授 伊犁师范大学
赵建平 教授 新疆大学
组织委员会:
张晓玲 教授 新疆大学
范兴亚 副教授 新疆大学
【日程安排】
报到时间:2025年7月21日
报到地点:伊犁师范大学
会议时间:2025年7月22日至7月26日
会议地点:伊犁师范大学
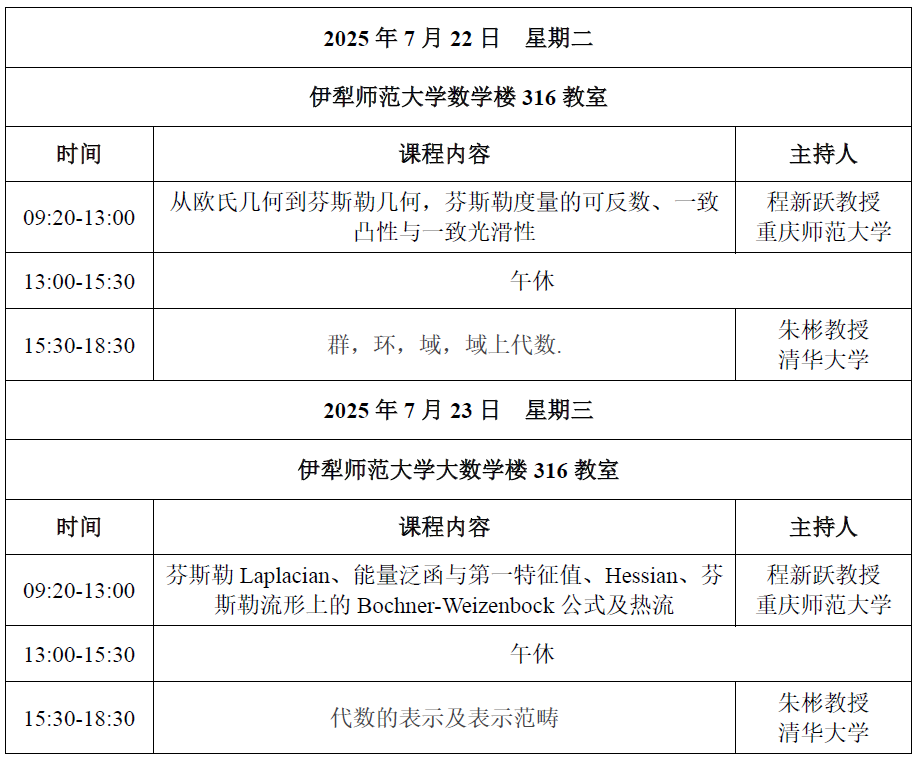
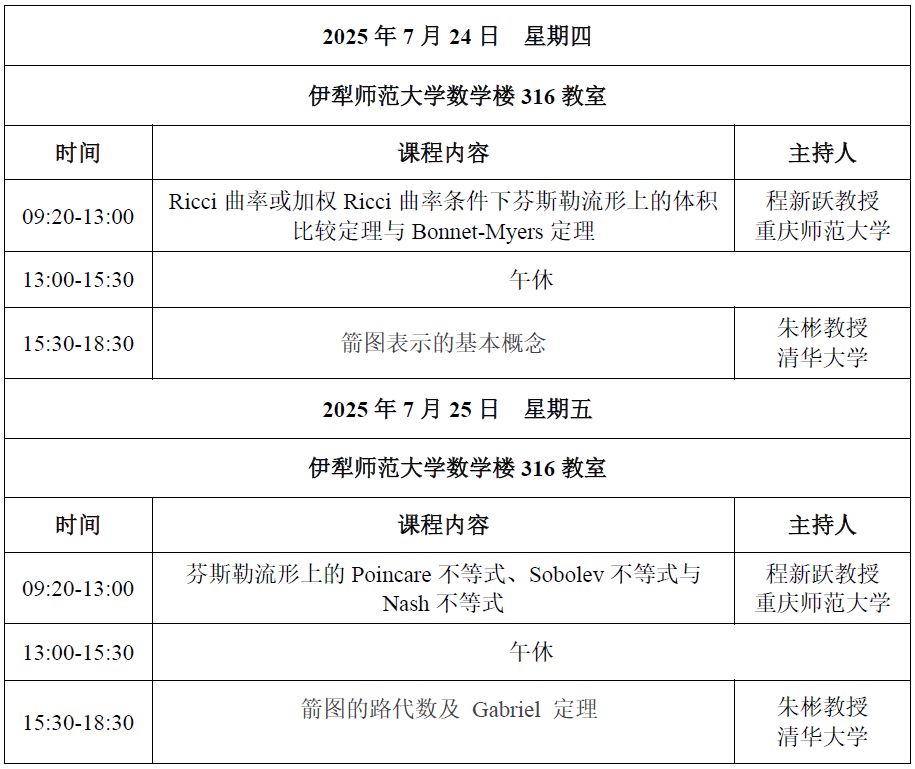

【课程简介】
几何系列讲座由重庆师范大学程新跃教授主讲
课程简介:
芬斯勒流形上的整体几何与分析是现代芬斯勒几何的一个重要组成部分,是将芬斯勒几何与偏微分方程、分析、拓扑紧密相连的一个重要的研究方向,近年来已得到了快速的发展。
本课程将着重介绍研究芬斯勒流形上的整体几何与分析所需的重要基本理论与方法,并介绍若干近期重要代表性研究成果及展望。主要内容包括:从欧氏几何到芬斯勒几何,芬斯勒度量的可反数、一致凸性与一致光滑性;芬斯勒Laplacian、能量泛函与第一特征值、Hessian、芬斯勒流形上的Bochner-Weizenbock公式及热流;Ricci曲率或加权Ricci曲率条件下芬斯勒流形上的体积比较定理与Bonnet-Myers定理;芬斯勒流形上的Poincare不等式、Sobolev不等式与Nash不等式;芬斯勒调和函数的均值不等式与Li-Yau梯度估计,热方程整体解的Harnack不等式与Li-Yau梯度估计。
代数系列讲座由清华大学朱彬教授主讲
课程简介:
我们课程的预定基础是:线性代数(矩阵与线性映射,线性变换);近世代数(群,环,域等基本概念及相关结论)。我们将从代数表示论中最基本的概念开始:首先回忆近世代数中的基本对象:群,环,域及其相关的基本结论;其次:介绍域k上代数,以及代数上的模(或称为“代数的表示”), 介绍代数的表示范畴即模范畴;我们将介绍相关的一些概念:如单模,不可分解模,投射模,内射模等;最后我们介绍箭图表示(quiver representation),它是一种特殊代数(箭图的路代数–path algebra)表示;将介绍著名的Gabriel分类定理。
1.群,环,域,域上代数。回忆近世代数中的群,环,域的概念,以及它们之间的同态基本定理;更多地关注各种具体的例子。介绍域k上代数的概念及例子,介绍关于域的基本结论。
2.代数的表示及表示范畴。介绍代数的模的概念(即“表示”), 介绍相关的基本结论;简单介绍范畴与函子等概念,引入代数的模范畴;
介绍代数表示论的基本任务。
3.箭图表示的基本概念。介绍箭图以及箭图表示,及其相关理论。
4.箭图的路代数及 Gabriel 定理。给定箭图Q,定义域k上的路代数 kQ,证明 kQ-mod与Q的表示范畴等价;介绍Gabriel 的有限表示型箭图的分类定理。
主要参考书:
1.章璞, 吴泉水:基础代数学,高等教育出版社
2.Harm Derksen, Jerzy Weyman, An introduction to quiver representations. GTM 184, AMS.
【联系人】
张晓玲 教授 新疆大学
Email:zhangxiaoling@xju.edu.cn
范兴亚 副教授 新疆大学
Email:fanxingya@xju.edu.cn